ネフティスガチャの考察

2017年2月10日 · in シャドウバース

最終更新：2017/02/10

だーれも気にしてないだろうけど、ネフティスガチャの確率を考察をします。
楽しいデッキですが、勝率が良くないイメージなのでこれを機に考え直したいと思います。



ネフティスについて

ファンファーレ
それぞれコストの異なるフォロワー（ネフティスを除く）をランダムに1枚ずつ、自分のデッキから場が上限枚数になるまで出す。この能力で出たフォロワーすべてを破壊する。

現行では特定のコスト帯に絞って確定でモルディカイを出現させるネフティスネクロや
コントロール系のフィニッシャーとして採用するコントロールネクロwithネフティスのようなデッキがあるが、
そもそもネフティスが出現した際の、「ランダムに1枚ずつ、自分のデッキから場が上限枚数になるまで出す」という処理はどのように行われるのか？

考えられる処理の仕方は2通りある。
①デッキ内のフォロワーリストを参照し場に出現させるコストを先に決定。次にそのコストの中から出現させるフォロワーを決定する。
②デッキ内からランダムにフォロワーを出現させる処理をし、続けて場が埋まるまでその処理を続けるが、2枚目以降は先に出たコストを除外する。
※どちらもネフティスは最初の処理の段階で除外することとする

例えばデッキの中にフォロワーが2・3・4・7・8のコスト帯のカードが入っていると仮定する。
この時①の方法で処理されている場合は、デッキに上記コストのカードが残っていれば、各コスト帯の出現確率は等しくなる。
しかし②の方法で処理されている場合は、偏りのあるコスト帯のカードの出現確率が高くなるため、各コスト帯の出現確率は等しくない。

以上のことからネフティスガチャを考慮するため、まずはどちらが正しいのかを確認します。



処理の仕方には運営から回答があった

実は調べてみると、本件について運営に問い合わせ、回答をいただいている人を発見することができた。

フォロワーの選択手順
1.選択の候補からネフティスを除きます。
2.デッキ内からランダムにフォロワーを選び、場に出します。この際、ランダムにコスト帯を選ぶのではなく、ランダムにカードを1枚選びますので、デッキに多く残っているカードがより選ばれやすくなっております。
3.選択の候補から2.で選ばれたフォロワーのコスト帯を除きます。
4.2-3を繰り返し、場が上限枚数になるか、デッキに選ばれるフォロワーがなくなった場合、そこで処理が終了します。

ということで、先に書いた予想②がネフティスガチャの処理の仕方であることがわかる。

ちなみに余談だが、ネフティスが追加されてしばらくはネフティスがランクマで使えなかったことがある。
この時ネフティスと一緒に、≪信仰の具現化≫≪祈りの集約≫という
デッキからランダムにカードを場に出すカードたちが制限されていたため
この段階で内部処理の仕方としては②が有力と考えていました。
(もちろん①の可能性もあるのですが、内部処理のアルゴリズム的には②の方が有力かなと素人的には思ってました)



ネフティス効果におけるモルディカイの出現確率について

計算の準備ができたところで、ネフティスガチャでモルディカイが出現する確率を求めたいのですが、
8ターン目までのムーブも考慮する必要がありかなり複雑なので、今回はざっくりした計算に留めます。
※正確な計算は要望と時間があればやりますが、確率計算よりも統計分析の方が相性よさげなのでデータが欲しい…
※自分の場はフォロワーがいない状態で、ネフティスを出したことにします。
※今回はモルディカイ出現のみ想定するため、出現順位に関する盤面状況など考察はしないです。

さて、今回はモデルデッキとしてこのデッキを使ってみます。

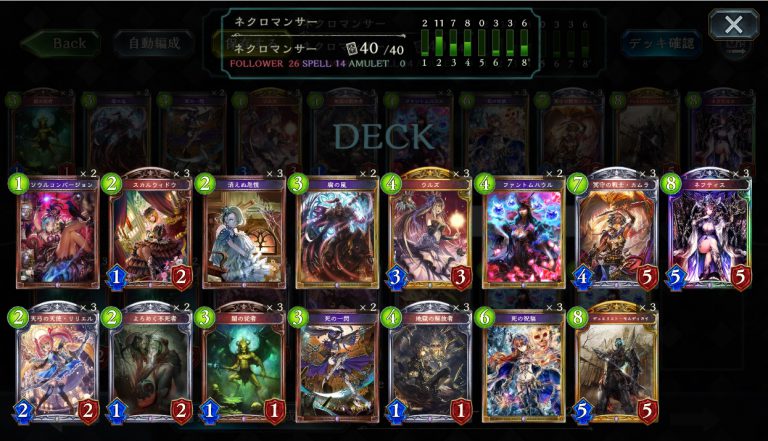
※普段使っているネフティスネクロデッキではないです

まず40枚ある状態でネフティスを使った場合、モルが出現する確率は58.26%であると計算できます。
予想①の処理であれば確率80％で出現してくれるため、実際はそれよりも低い確率になってしまいます。

では、8ターン目ネフティス(先攻11枚・後攻12枚を引いたあとのネフティス)ならばどうなるのか？

今回のモデルデッキの場合はフォロワー数とフォロワー以外の枚数の比率が26：14ののため、
期待値理論で計算すると、8ターン目までに先攻は6.83枚・後攻は7.45枚のフォロワーを引いていることになります。

次に8ターン目までにどのコスト帯のフォロワーを何枚引いているのかを考慮したいのですが、
先ほど求めた小数の枚数のまま、どのコスト帯も等しい確率で引いていると仮定すると、モルの出現確率は58.26%になります。
ですので、計算が苦手な人やざっくりでかまわない人は、
40枚計算のモルディカイの出現確率＝8ターン目ネフティス効果のモルディカイ出現確率
と考えても大丈夫です。

さて、とは言っても実際にはマリガンという行為があります。
マリガンでは2コス(3コス)を優先的に引くことになるため、2コス(3コス)のドロー比率は他コストより高くなります。
そのため今回は最初に2コス1枚をマリガン時に保有していると仮定して、以下2パターンについてそれぞれ考察してみます。
※先攻と後攻の場合分けが面倒なので、8ターン目までにフォロワーを7枚引いた想定に統一します。

パターン1）2コス3枚、4コス2枚、3コスまたは7コス1枚、ネフ1枚
パターン2）2コス3枚、4コス2枚、ネフ1枚、モル1枚

計算してみると、パターン1は76.47%・パターン2は52.94%の確率でそれぞれモルディカイが出現します。
40枚時に計算したものよりも、低コストのドロー比率が高い想定で計算するとその分フォロワーが圧縮され確率が上がります。
ネフティスを出す前にモルを引いてしまっても、40枚時の確率に近い確率で出現するため悪くはないかもしれません。

パターン1は3コス・7コスの2通りがあるので、それを考慮しつつパターン2と平均を取ると
ざっくり71.66％の確率でモルディカイが出現することがわかります。
※ほんとざっくり計算なので数学的に正しくない結論なのは許してください



総評

ネフティスは確定デッキでなくてもフォロワー率を調整することで7割近くの確率でモルディカイを呼べることがわかりました。
実際はネフティスを引かなければならないのでその確率も考慮すると、マリガン時にネフティスを保持するとして、
およそ5割の確率でネフティスからのモルディカイが実現することがわかります。

8ターン目に素出しのモルディカイもアリと考えると、8割近い確率で8ターン目にモルディカイが出現します。
ちなみに確定デッキの場合でもネフティスとモルディカイを引き当てる確率が必要なため、8ターン目モルディカイ出現は9割くらいです。

そう考えると、8ターン目のモルディカイ出現確率に大きな違いがないと捉えられるなら
確定デッキは序盤の動きが不安定になりがちなため、あえて不確定なデッキを構築した方が勝率はいいかもしれません。

ただ確定デッキは、ネフティスの際に何が出るか予想できるため、
後半のムーブが運にならないという意味ではやっぱり強いと思います。

どちらもメリット・デメリットがあるのは当然なのですが、
不確定デッキは言うほどモルディカイが出現しないわけではないとわかりましたので、
デッキ構築やプレイングの参考にしていただければと思います。

※割とざっくり計算しているため誤差は許してください。ただ大きく値が違うのは計算ミスです。あれば教えてください。